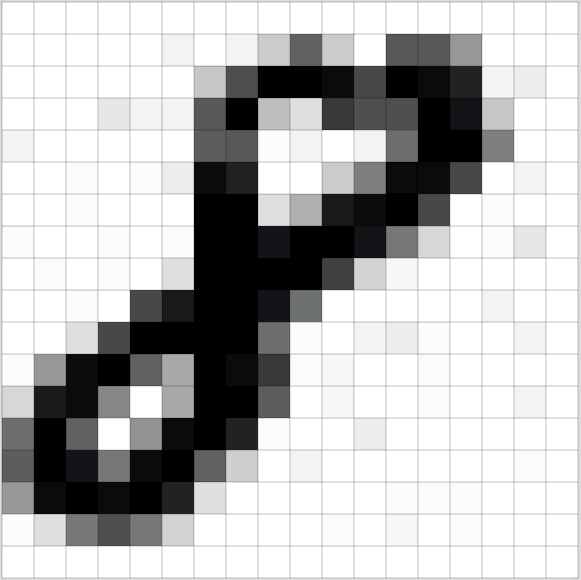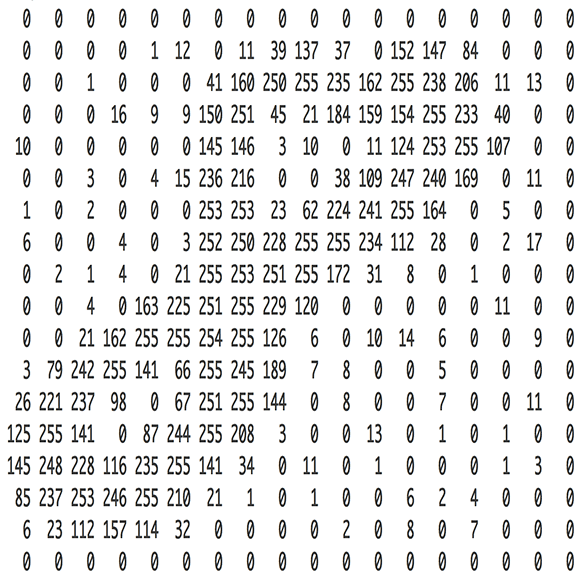《机器学习有意思! 03》- 深度学习与卷积神经网络
《机器学习有意思! 03》- 深度学习与卷积神经网络
原文:Machine Learning is Fun! Part 3 – Deep Learning and Convolutional Neural Networks
作者:Adam Geitgey
你是否厌倦了每天被深度学习相关的新闻轰炸却不明所以?此诚求变之机。
这一次我们将学习如何用深度学习来写程序识别图像中的物体。也可以说我们是要解释Google图片搜索背后的黑科技:Google可以通过描述搜索图片——即使图片没有事先打上标签!这是如何实现的?
就像Part 1和Part 2一样,本指南仍然面向所有对机器学习感兴趣却不知如何开始的朋友们。我们的目标是所有人都读得懂——因而势必无法照顾到每个细节。但那又如何呢?只要能让一位读者对ML感兴趣,那就是功德一件了!
深度学习识别物体
产品:每当一名用户拍了照片,APP应该检测他们是否在国家公园……
开发:当然了,不过是简单的GIS查询而已,给我几个小时。
产品:……以及拍的是不是一只鸟。
开发:那我需要一个研究小组和五年时间。
旁白:在计算机科学中,有时很难解释“简单”和“根本不可能”之间的区别。
你可能已经在xkcd系列漫画中看到过了。
这里的笑点在于,三岁小孩儿都能认出鸟的照片,但是教会计算机识别物体,已经让最优秀的计算机科学家耗费了50年。
在过去的几年里,我们终于找到了物体识别的好路子,那就是深度卷积神经网络。这听起来像是从威廉·吉布森的科幻小说里捡了几个词拼起来的,不过只要分解开来细看,其原理真的很简单。
开始吧——现在就写一个能认识鸟的程序!
始于足下
在我们学习如何辨别鸟的照片之前,先来学个简单得多的例子——手写数字”8”。
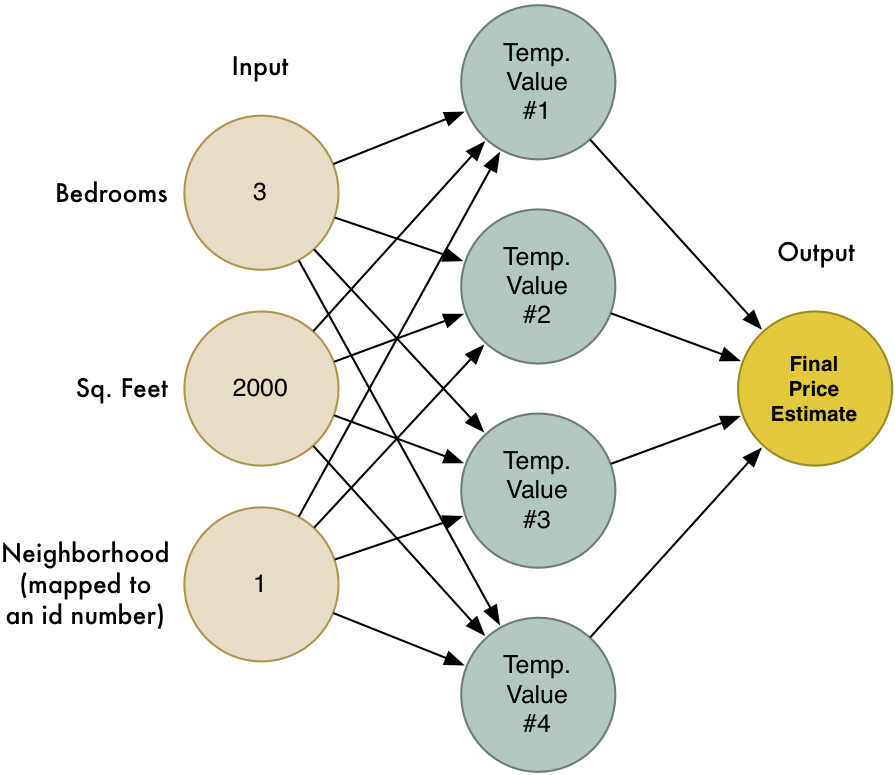
在Part 2中,我们已经学习了神经网络如何链接大量的神经元来解决复杂问题。我们搭建了一个迷你神经网络来基于房间数、面积、周边环境预测房价:
我们还知道了机器学习的思想就是重复利用相同的普适算法,根据不同的数据,解决不同的问题。下面我们修改这个神经网络来识别手写文本,并且进一步简化任务——只识别数字”8”。
机器学习只有当你有数据的时候才好使——数据越多越好,所以我们需要大量的手写”8”来开始。所幸,研究者们为了这一目的已经建立了MNIST手写数字数据集。MNIST提供了60,000张手写数字的图片,每个尺寸都是18x18,以下是数据集里部分的”8”:
其实不过是数字
Part 2里搭建的神经网络只读取3个输入(”3”间卧室,”2000”平方米等)。但是现在我们要用神经网络处理图片,不是数字怎么传入神经网络呢?
答案无比的简单。神经网络以数字为输入,对于计算机来说,图片也不过只是代表了像素明暗的数字:
只要把18x18像素的图片当作324个数字组成的数组,就可以把图片输入给神经网络了。
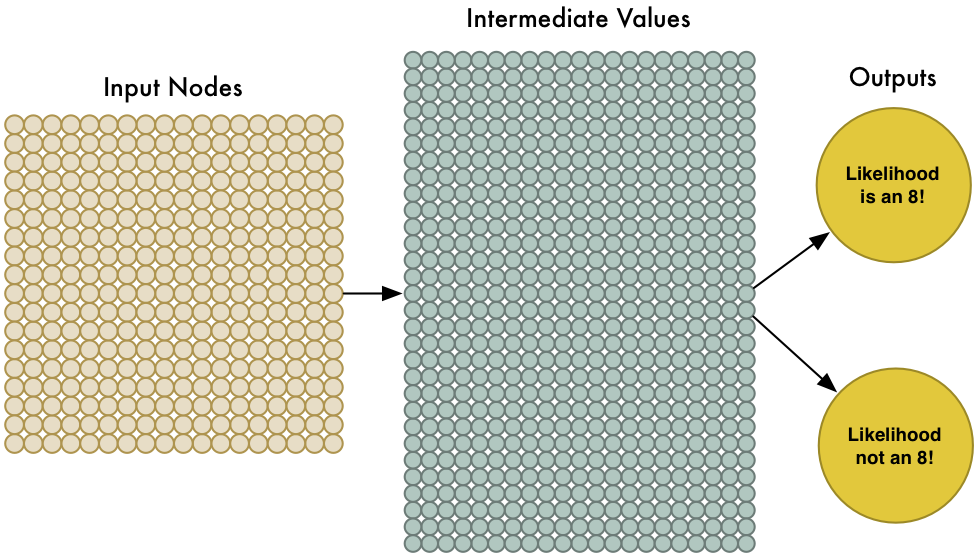
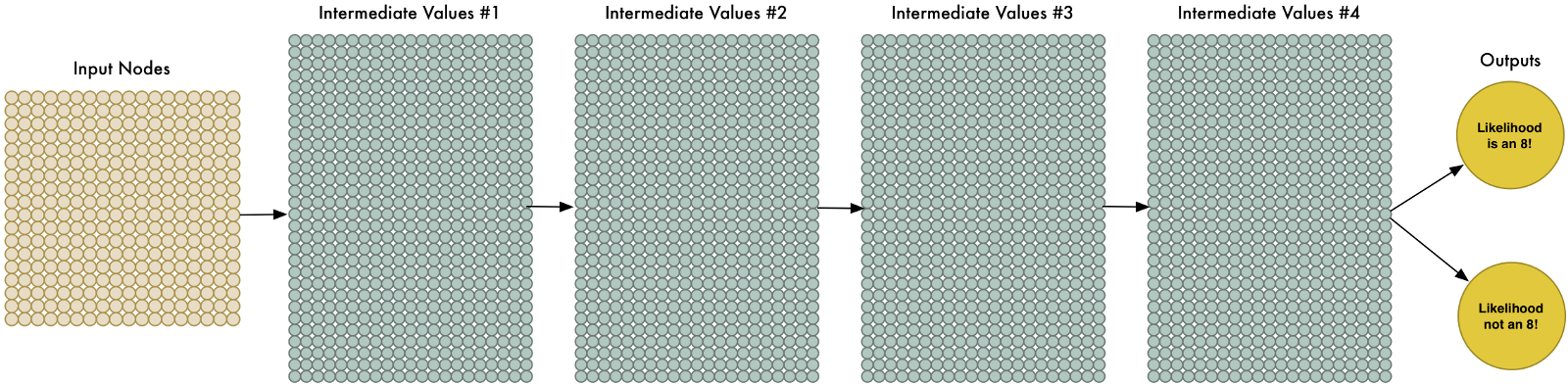
要处理324个输入,我们只需让神经网络具有324个输入节点:
注意我们的神经网络现在有两个输出(而非之前的一个)。第一个输出是预测此图为”8”的概率,第二个为不是”8”的概率。每种类型的目标物体有了分别的输出,就可以让神经网络对物体进行分类了。
这次的神经网络比之前要大得多了(从3个输入到324),但是现代的计算机处理几百个节点的神经网络,连眼都不带眨的,甚至连手机都能轻松满足。
剩下的就是用”8”和非”8”的数字去训练神经网络以使其能够区分两者了,当我们输入一个”8”,我们告诉神经网络,此图为”8”的概率是100%,非”8”的概率是0%,反之亦反。
这是我们的训练数据:
现在随便一个笔记本电脑,也能在几分钟之内训练完这样一个网络,训练完之后我们就拥有了能够高精度识别数字”8”的神经网络。欢迎来到(1980年代的)图像识别世界!
管窥
把像素简单地导入神经网络里一训练,就能识别图像了,感觉无比清爽。机器学习真乃魔法……也?
事情并不简单。
首先,一个好消息是,我们的识8器对于图片正中的数字,效果还是很喜人的:
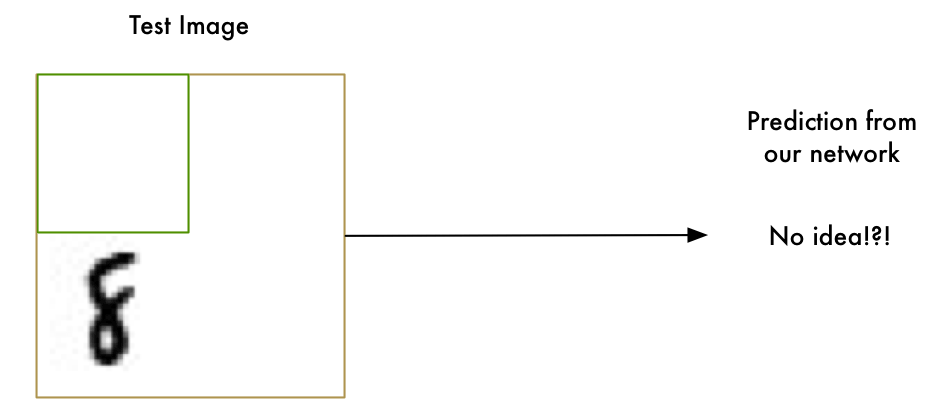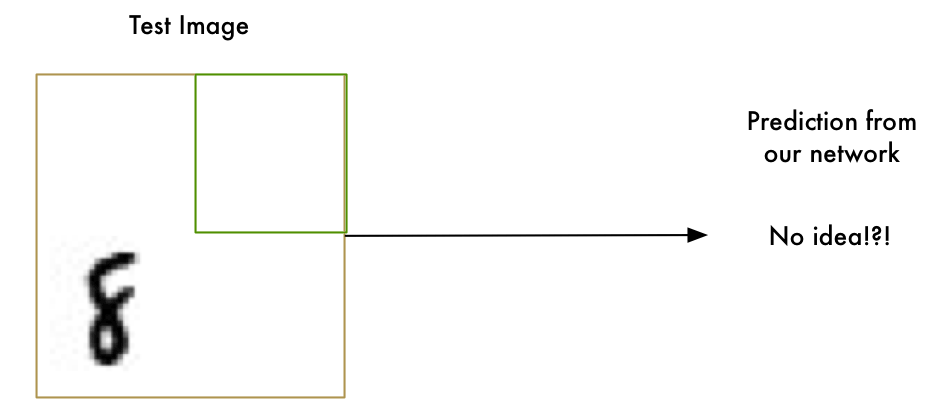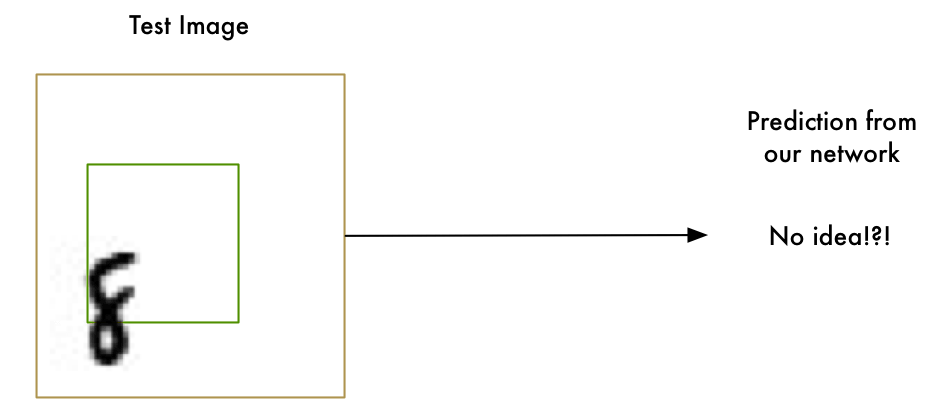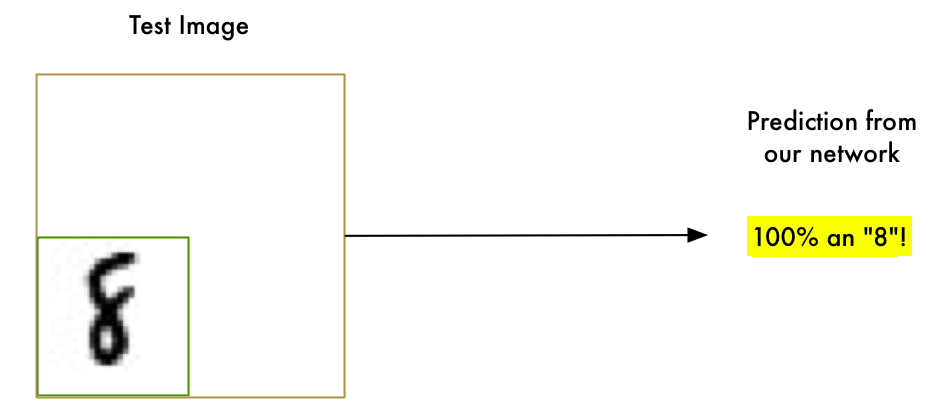
现在坏消息来了:
当数字不是恰好居中的时候,识8器完全失效了,哪怕一丁点的位置偏差也不行:
这是因为,神经网络只学到了恰好居中”8”的模式,但是对于离心的”8”却一无所知,它知道且仅知道一种模式。
在现实中这就实用价值不大了,因为实际问题不可能总是那么干净简约。所以我们必须让神经网络能够处理离心的”8”。
暴力方法 1. 滑动窗口搜索
我们已经有了一个好方法,能够找到图片中心的”8”,那可不可以在图片上扫描寻找子区域里的”8”,直至找到呢?
这就是滑动窗口法,一种非常暴力的解决方案。在很有限的某些例子中可行,但效率也很低。你必须一遍一遍地寻找不同尺寸的物体,我们可以比这更好。
暴力方法 2. 更多数据,更深网络
当我们在训练网络的时候,只用到了完美居中的”8”。如果我们在训练过程中就引入不同位置、不同大小的”8”,那会怎么样呢?
不需要收集更多的训练数据,我们可以写个脚本生成新的图片,图中的”8”具有不同的位置和大小:
应用这一技术,我们可以轻易创造出无穷多的训练数据。
更多的数据让问题变得更加复杂了,但是我们可以用更大的神经网络,那样就能学习更复杂的模式。为了扩大网络,我们简单地把节点层堆叠起来:
这就是“深度神经网络”,因为比传统神经网络的层数更多。这个想法在1960年代便有了,不过直至最近,训练这么大的神经网络训练还是慢得无法接受。但是自从我们发现了用3d显卡替代传统CPU来加速矩阵计算,大规模神经网络就变得可行了。你用来玩守望先锋的NVIDIA GeForce GTX 1080显卡,也可以用来训练神经网络。
然而即便我们可以用显卡很快地训练出大规模神经网络,这仍然不是解决方案的全部,我们还需要在处理图片上更加机智才行。
在暴力方法2中,把图片顶端的”8”和图片底部的”8”当作完全不同的物体,这其实是没有意义的。应该存在一种方案,让神经网络不经额外训练即知:图片不管哪个位置的”8”都是一个东西。万幸,确实是存在的!
答案:卷积
生而为人,你可以直观地看出照片中含有层次或概念结构。考虑这张照片:
作为一个人类,你立即就能识别出照片里的层次:
地面覆盖了草坪
图里有个小孩儿
小孩儿骑在弹跳小马上
弹跳小马在草坪上
更重要的是,无论小孩在什么样的表面上,我们都能认出那是个小孩儿。我们并不需要重新学习各种表面上的小孩儿。但是目前,神经网络还做不到这些,它会把不同位置的”8”当作完全不同的东西,而并不知道在图片上移动物体不会改变其实质。这意味着网络必须重新学习每个位置上的物体,太悲催了。
我们需要让神经网络明白平移不变形——“8”还是”8”,不论出现在图片的哪里。这一过程可由卷积实现,卷积的想法部分来自计算机科学,还有部分是受生物学启发(比如,疯狂科学家们真的在猫脑子里插管,以研究猫是怎么处理图像的人)。
卷积的作用机理
这次我们不再把整个图片当成一个数字网格输入到神经网络,而是利用物体与位置的独立性,做得更聪明些。以下就是卷积的作用机理,一步一步来——
第1步:把图片分解为重叠碎片
与之前的滑动窗口法类似,这里也用一个窗口在整张原图上滑动截图,并且把截到的每一小部分单独存成一个图片:
如此我们便把一张大图拆成了77张等尺寸的小图。
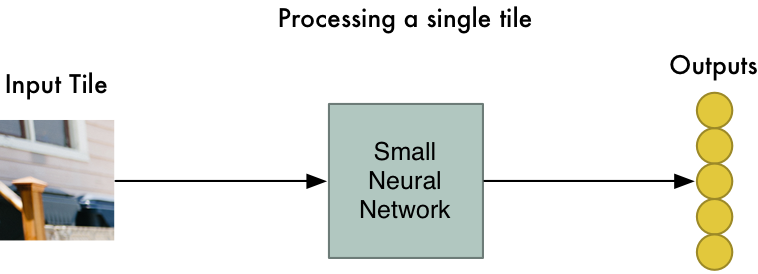
第2步:把每张小图输入小神经网络
曾经我们把单张图片输入神经网络来判断其是否为”8”,这里再重复一样的工作,不过是针对每一个单独的小图片:
这里还有一大诀窍:我们将相同的神经网络权重应用在每一块小图上。换言之,我们平等地对待所有小图,如果某个小图里出现了我们感兴趣的内容,我们就将其标记为有趣。
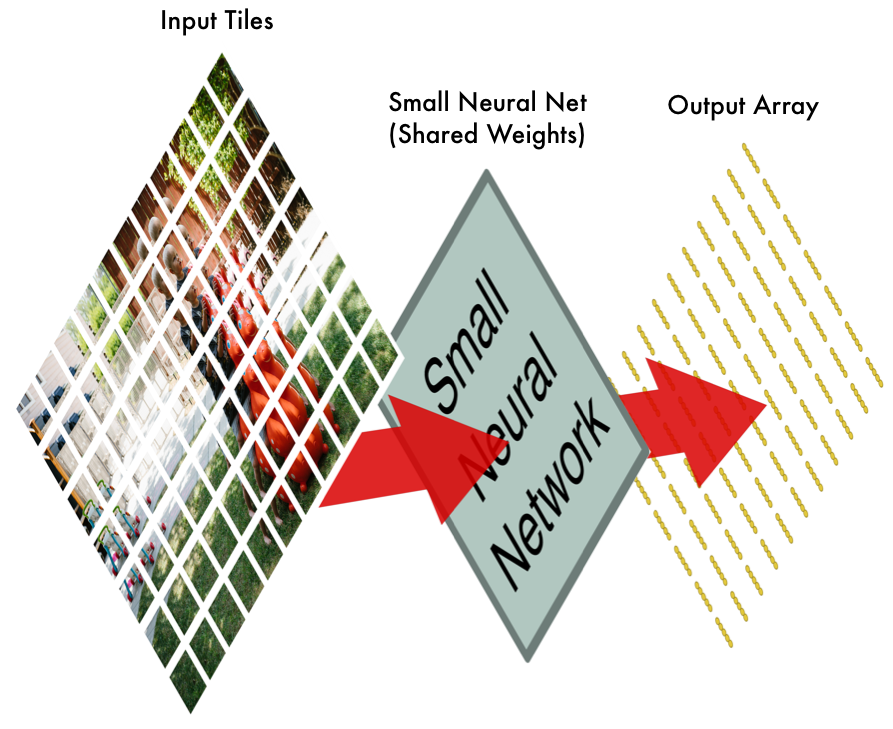
第3步:把每块小图的结果存入新的阵列
我们并不想丢失原始小图的排列信息,所以我们要把每个小图的结果按照相同的排列重新构建原图,形式如下:
也可以说,我们从一张大图片开始,到小阵列结束,阵列记录了原图当中哪一部分有我们最关心的内容。
第4步:下采样
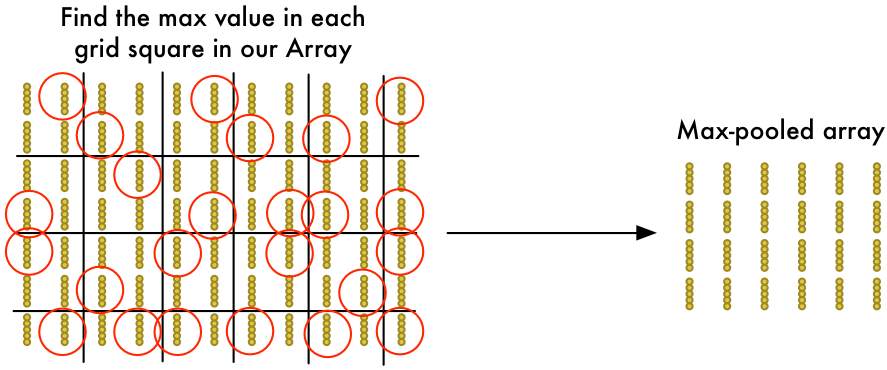
第3步的结果是一个阵列,反映了原图的哪一部分是我们最感兴趣的,不过这个阵列仍然很庞大:
为了减小阵列的尺寸,我们用最大池化算法进行下采样。听着很稀奇,其实完全不!
看阵列中的每个2x2方块,并且只留下最大的数字:
这里的主要思路就是,当我们在组成2x2方块的四个输入小图中的任意一个发现了关心的内容,就只保留我们最感兴趣的信息,这可以减小阵列规模并保留最重要的信息。
最终步:预测
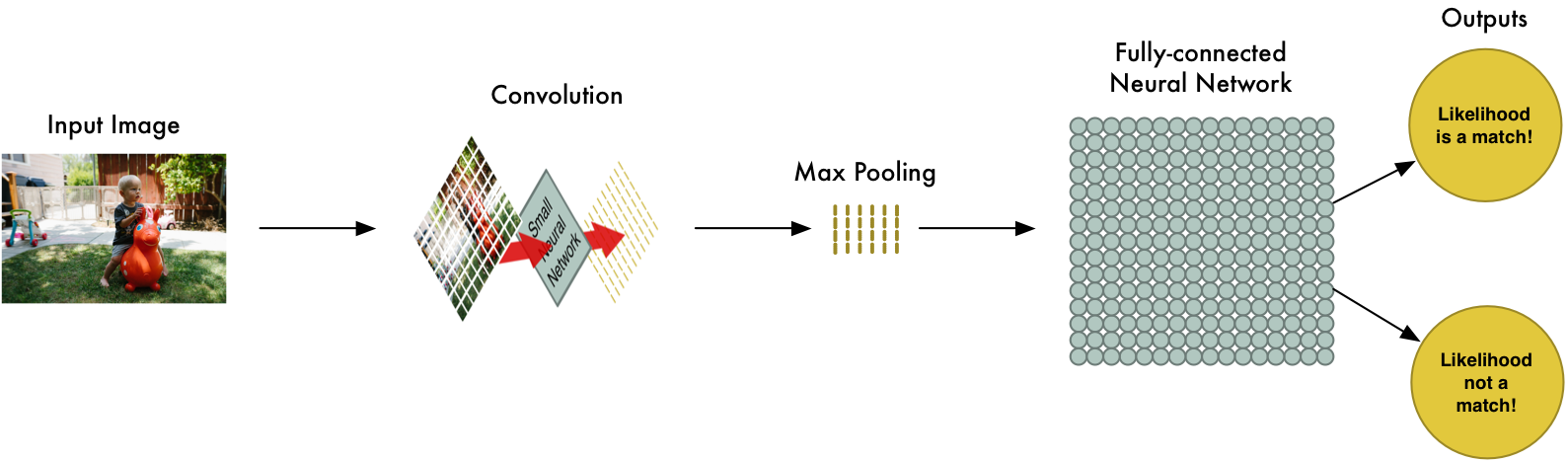
至此,我们已经把一个巨大的图片消减成了相对较小的阵列,阵列就是一串数,所以我们可以把小阵列输入另一个神经网络,最后的这个神经网络会决定图片是否匹配。为了与卷积层相区分,我们称之为“全连接层”。从头到尾,我们的五步流水线如下图所示:
增加更多步骤
我们的图像处理流水线有一系列步骤:卷积,最大池化,全连接网络。
而在解决实际问题的时候,这些步骤可以组合起来并堆叠多次。你可以加两个,三个甚至十个卷积层,也可以在任何时候插入一个最大池化层。总之基本思路就是把一张大图,逐步分解为小图,直至我们能够获得结果。卷积层越多,网络就能学习识别越复杂的特征。
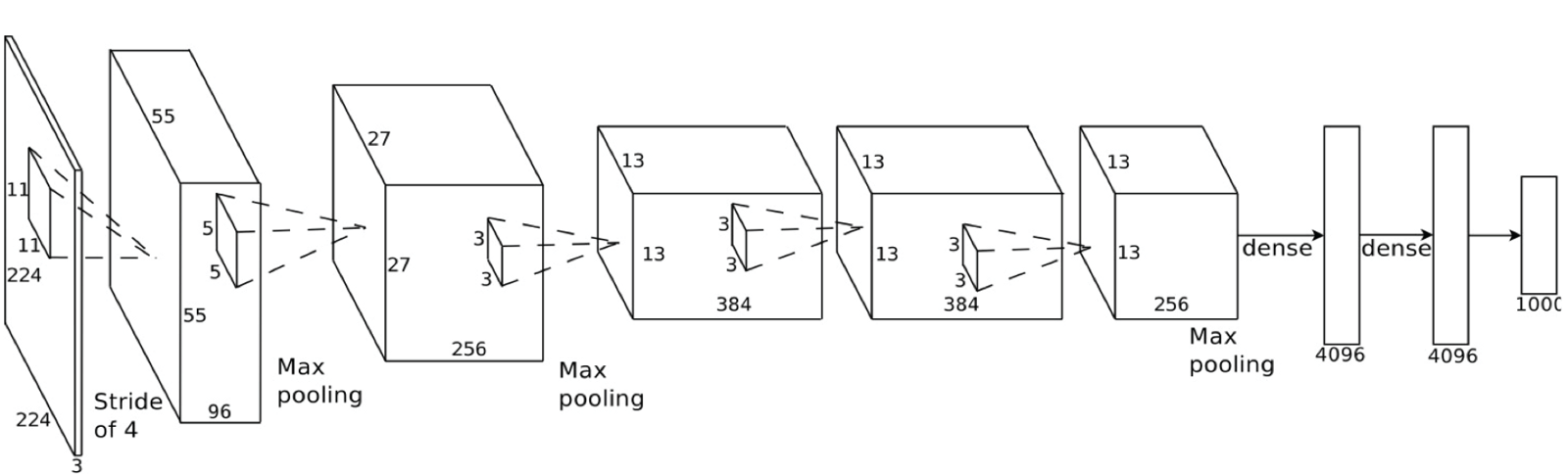
比如说,第一个卷积层可能学会了辨认锐利边缘,第二个卷积层可能根据锐边的知识学会了识别鸟喙,第三个卷积层又基于鸟喙识别出了整只鸟。以下是更贴近实践的深度卷积网络结构(学术论文里常见):
在这一实例中,他们从224x224像素的图片开始,应用了:卷积,两次最大池化,三次卷积,又是两次最大池化,最后是两个全连接层。最终的结果可以将图片从1000个分类中识别出来。
构建正确的网络
那么我们要怎么知道什么时候该用什么层呢?诚然,你得经过大量的实践和测试才能回答,可能训练100个网络才能找到最佳的结构和参数。机器学习就是包含了大量的尝试和错误!
构建鸟分类器
如今我们已经足以写出一个程序来判断一张图上是不是鸟类。一如既往,我们需要训练数据来开始。免费的CIFAR10数据集包括了60,000张鸟类图片和52,000张非鸟图片。如果要更多的数据,我们还需要加入Caltech-UCSD Birds-200-2011数据集,内含12,000张鸟类图片。
这是组合数据集的一部分鸟图:
以及一部分非鸟图:
这一数据集可以很好地满足我们的需求,不过相对于真实世界的应用而言,72,000张低分辨率图片还是太少,如果你想要达到Google级的水平,你需要上百万张高清无码大图。在机器学习中,数据多总是比算法好更重要。现在你就知道Google为什么那么乐意提供无限照片存储了,他们要的是你的数据啊,数据!
原作者使用的是TFLearn,译注者改用了国内更流行的Keras。TFLearn代码可见作者原文。
Keras封装了TensorFlow和Theano两个深度学习库并提供了简单易用的API,这使得开发者可以仅用几行就搭建一个卷积神经网络。
以下是定义并训练网络的代码:
导入数据
Keras内置了CIFAR10数据集,但是需要从网络上下载。
Keras导入CIFAR10数据集:
1 | # 导入相关库 |
搭建神经网络
下面导入其他将会用到的Keras相关模块并对数据进行预处理。Keras搭建神经网络的过程其实非常简单直观,就像搭积木一样。
首先确定网络的基本结构,这里就用最基本Sequential()串型拓扑,并建立网络模型对象model。
之后便是给model中一层层地添加网络,添加的方式也很简单,就是使用model.add()方法,逐个地把卷积层(Convolution2D)、池化层(MaxPooling2D)、全连接层(Dense)等插入到model里,形成整个神经网络。
Keras搭建神经网络
1 | # 对标签进行独热码编码 |
编译、训练、预测
经过以上过程,我们已经有了一个神经网络的外壳,但也仅仅是外壳,你会注意到上面这个代码模块运行的很快,因为这只是根据神经网络的设置形成了一个容器,内部还是空空如也。还要经过“编译”并且导入数据进行“训练”,我们才真正拥有了“有血有肉”的神经网络。最后通过与测试集的对比,衡量神经网络的表现。
虽然数据量并不大,但是训练神经网络对于普通CPU来说,还是个比较艰巨的任务,因此训练速度可能堪忧。我们的网站后台暂时还未提供GPU接口,所以这里只能先将训练迭代次数设为1,以后我们会争取提供更强大的计算资源。
1 | # 设定训练过程 |
如果你有个不错的显卡和足够的显存(比如Nvidia GeForce GTX 980 Ti或以上),大概一个小时可以训练完,如果用CPU的话可能就要久的多了。
精度随着训练进程儿上升。第一轮过后,我的精度只有75.4%;经过十轮,精度已经提高到91.7%;在50轮以后,精度攀升到95.5%,再训练已经收效甚微了,因此我就此打住。
Congrats!现在我们的程序可以识别图片里的鸟了!
测试网络
有了训练过的神经网络,是骡子是马该拉出来遛遛。这一简单的脚本读取一个图片文件并判断是否是鸟。
为了真正检验我们的神经网络是否有效,需要测试大批的图片。我这里用了15,000张图片作为验证集,当我把这15,000张图传递给神经网络,95%都得到了正确答案。
听起来很好,对吧?其实这可未必!
95%是多准确?
我们的神经网络号称有95%的准确度,但是细微之处见真章,面子上95%,里子可能千差万别。比如说,如果我们的训练图片里5%是鸟,而另外95%不是鸟,然后一个程序只输出“不是鸟”就可以达到95%的精度,但这毫无意义。
我们需要进一步细究这个数字,而不是满足于一个含糊的95%。为了判断一个分类系统的作用究竟几何,我们需要考察它是如何失效的,而不是失效的百分比。抛掉单纯的“对/错”标准,我们来把问题细分为四种分别的情况——
- 把鸟正确地识别为鸟:True Positives
- 把不是鸟的正确地排除出去:True Negatives
- 以为是鸟,结果不是:False Positives(错杀三千)
- 其实是鸟,以为不是:False Negative(放过一个)
根据我们这15,000张图片,以下为各种情况的统计数据:
为什么要这样细分结果呢?因为并非每种错误都是均等的。想象一下,如果我们在写一个根据MRI图像诊断癌症的程序,这时候宁可引入False Positive也不要带有False Negative。前者只是让患者虚惊一场,后者可就是延误治疗了。
所以出了宽泛的准确度,我们还计算精确率和召回率。精确率和召回率更加清晰地定义了分类起的效用。
由上表可知,当我们给出“是鸟”的猜测时,其中97%是对的。但是我们却只找出了90%的鸟,这意味着我们可能不是所有鸟都认得,但是认鸟却很准!